画像の表現
Python で画像を表現してみましょう。
白黒の表現
東京大学がアルゴリズム入門の授業用に作った ita ライブラリを使えば、簡単に画像を表現できます。(ita って、Introduction to Algorithms の略なんですかね?)
ita ライブラリは、インストールして使う必要があります。ライブラリをインストールするには、先頭で !pip install ita と書けば良いのでした。
ita ライブラリで画像を扱う場合は、次のようなコードをはじめの方に書いておく必要があります。これに関しては、おまじないだと思ってください。Google Colaboratory 上でうまく表示するために、必要になっています。
%matplotlib inline
次のように、0 と 1 が格納された二次元配列を作って、それを ita ライブラリの image_show 関数に与えれば、白黒の画像を表現できます。0 が黒、1 が白となります。
練習問題
ita ライブラリを使って次のような画像を作ってみましょう。
グレースケール
0 から 1 の間で数値を変化させることで、グレースケールを表現することもできます。
カラー画像
赤、緑、青の順に 0 から 1 の範囲で指定することで、カラー画像を表現することもできます。
光の三原色は、赤、緑、青です。この 3 つを混ぜることで、すべての色を表現することが可能です。加法混色なので、赤、緑、青をすべて合わせると白になります。
これを使った色の表現法が、RGB です。これは、赤(Red)、緑(Green)、青(Blue)の頭文字となっています。
コンピューターでは、0 から 255 の 256 段階でそれぞれの色を表すので、 通りの表現が可能です。
色にも三原色があります。 色の三原色は、シアン、マゼンタ、イエローです。減法混色なので、シアン、マゼンタ、イエローをすべて合わせると黒になります。
これを使ったのが、CMYK です。インクなどに使われます。これは、シアン(Cyan)、マゼンタ(Magenta)、イエロー(Yellow)の頭文字です。K は BlacKからだと言われますが、キープレート(Key plate)からだそうです。K が入っているのは、インク代を節約するためと綺麗な黒を表現するためです。
練習問題
次のような画像を作ってみましょう。
練習問題
練習問題 1
左から右にかけて、黒色から緑色に色が変化するグラデーション画像を作ってみましょう。
配列.append(要素) とすることで、配列の末尾に要素を追加できます。
ヒント
左側が黒で右側に行くにつれてだんだん緑になるように、数値を少しずつ変化させていけば良さそうです。
二次元配列の作り方としては、まず空の配列を作り、それに append を使って値を入れていき一次元配列を作ります。
さらに、これを空の配列に入れていけば、二次元配列になります。
練習問題 2
左から右にかけて、白色から青色に色が変化するグラデーション画像を作ってみましょう。これは、少し難しいです。分からなかったら、ヒントを見てください。
ヒント
次のように、加重平均をとると、うまくできます。
右側の色と左の色を定義して、その加重平均をとるという流れになるかと思います。
練習問題 3
左上が白、右上が赤、左下が緑、右下が青となるようなグラデーション画像を作ってみましょう。
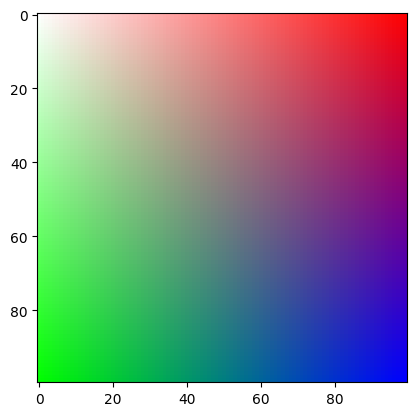
ヒント
次のように、二次元で加重平均をとると、うまくできます。

